Traverse by Graph

Elements in graph model will form another graph structure according to connection relation, also called graph. The node means the middle point in the graph. The edge represents the edge in the graph. The traversal that Qunee supports the nodes in the graph. It may also be applied to automatic layout method

• #forEachByTopoDepthFirstSearch(call, scope, postOrder) - Depth first traversal of graph, supports preorder and postorder traversal which is defaulted to preorder traversal

• #forEachByTopoBreadthFirstSearch(call, scope, postOrder) -Breadth first traversal of graph, supports preorder and postorder traversal which is defaulted to preorder traversal

The topological structure is showed in the following graph. The arrow indicates the edge direction. Different call sequences will be realized by different traversal method

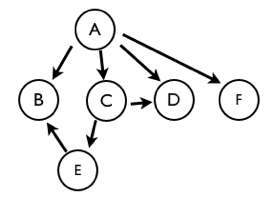
Example

var model = graph.graphModel;
var a = model.add(new Q.Node('A'));
var b = model.add(new Q.Node('B'));
var c = model.add(new Q.Node('C'));
var d = model.add(new Q.Node('D'));
var e = model.add(new Q.Node('E'));
var f = model.add(new Q.Node('F'));
model.add(new Q.Edge(a, b));
model.add(new Q.Edge(a, c));
model.add(new Q.Edge(a, d));
model.add(new Q.Edge(c, d));
model.add(new Q.Edge(c, e));
model.add(new Q.Edge(e, b));
model.add(new Q.Edge(a, f));
 
Q.log('forEachByTopoDepthFirstSearch by pre-order');
model.forEachByTopoDepthFirstSearch(function(node){
    Q.log(node.name);
});
Q.log('forEachByTopoDepthFirstSearch by post-order');
model.forEachByTopoDepthFirstSearch(function(node){
    Q.log(node.name);
}, null, true);
Q.log('forEachByTopoBreadthFirstSearch by pre-order');
model.forEachByTopoBreadthFirstSearch(function(node){
    Q.log(node.name);
});
Q.log('forEachByTopoBreadthFirstSearch by post-order');
model.forEachByTopoBreadthFirstSearch(function(node){
    Q.log(node.name);
}, null, true);
 

Print results:

forEachByTopoDepthFirstSearch by pre-order

A

B

C

D

E

F

forEachByTopoDepthFirstSearch by post-order

B

D

E

C

F

A

forEachByTopoBreadthFirstSearch by pre-order

A

B

C

D

F

E

forEachByTopoBreadthFirstSearch by post-order

B

E

C

D

F

A